Рекомендации по повторяемым последовательностям случайных чисел

Создавая что-либо процедурное, вы практически гарантированно столкнётесь с необходимостью применения случайных чисел. И если вы захотите, чтобы один и тот же результат выдавался больше одного раза, вам потребуются повторяемые случайные значения.

В этой статье в качестве примеров будет использоваться генерация игровых уровней/миров, но эти уроки применимы и к таким вещам как процедурные текстуры, модели, музыка и т.д. Однако, это не касается областей с чётко определёнными требованиями, вроде криптографии.

Зачем может понадобиться повторять один и тот же результат?

• Возможность заново посетить тот же уровень/мир. Например, определённый уровень/мир создаётся из специфического сида. Используя тот же сид, вы снова получите тот же уровень/мир. Это можно сделать, например, в Minecraft.
• Постоянный мир, генерируемый на лету. Когда мир генерируется по ходу того как его изучает игрок, может понадобиться, чтобы уже посещённые локации оставались прежними (как в Minecraft или грядущей No Man’s Sky), а не менялись каждый раз, как во сне.
• Один мир для всех. Вероятно, вы захотите, чтобы мир был одинаковым для всех игроков, как будто он не был сгенерирован процедурно. Именно так и устроена No Man’s Sky. Тут почти как и в случае с возвращением в посещённый уровень/мир, кроме того момента, что всегда используется один сид.

Мы несколько раз упомянули слово «сид». Сидом (seed) может быть число, текстовая строка, или другие данные, используемые как входное значение для получения случайного результата на выходе. Отличительной чертой сида является то, что один и тот же сид всегда выдаёт одинаковый результат, но даже малейшее его изменение может привести к совершенно иному результату.

В этой статье мы рассмотрим два разных способа получения случайных чисел – генераторы случайных чисел и случайные хеш-функции – и причины для выбора одного или другого. Эти знания дались мне непросто, и подобную информацию сложно найти в свободном доступе, так что я решил, что просто обязан написать эту статью и поделиться ей.

Генераторы случайных чисел

Наиболее простым способом получения случайных чисел являются генераторы случайных чисел, или ГСЧ. Во многих языках программирования есть классы и методы ГСЧ со словом random в названии, так что они будут очевидной отправной точкой.

Генератор случайных чисел выдаёт последовательность случайных значений в зависимости от исходного сида. В объектно-ориентированных языках ГСЧ – это обычно объект, инициализирующийся с помощью сида. После этого метод объекта может повторно вызываться для генерации случайных чисел.

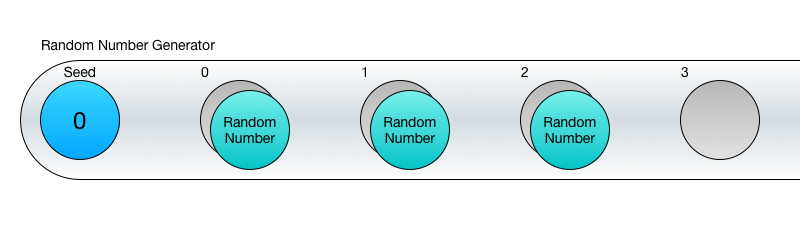
Код на C# будет выглядеть примерно так:

Random randomSequence = new Random(12345);
int randomNumber1 = randomSequence.Next();
int randomNumber2 = randomSequence.Next();
int randomNumber3 = randomSequence.Next();

В данном случае мы получаем случайное целое число от 0 до максимально возможного целого (2147483647), но вам не составит труда назначить результатом случайное целое число из нужного диапазона или случайное число с плавающей запятой от 0 до 1. Есть немало методов, делающих это самостоятельно.

Вот изображение первых 65536 чисел, сгенерированных классом Random в C# из сида 0. Каждое число представлено пикселем с яркостью от 0 (белый) до 1 (чёрный).

Здесь важно понимать, что вы не сможете получить третье случайное число, пока не получите первое и второе. Это не просто недосмотр в реализации, такова сама суть ГСЧ – он генерирует каждое новое число, используя предыдущее в своих вычислениях. Поэтому мы и говорим о случайной последовательности.

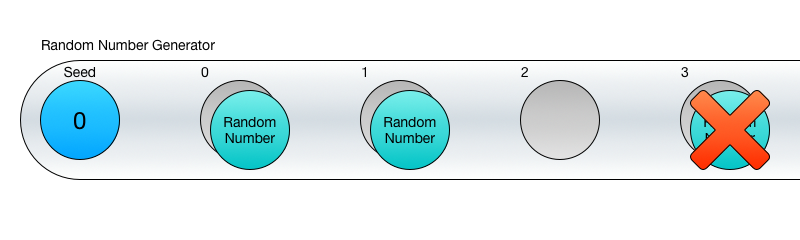
Это значит, что пока вам требуется несколько идущих по порядку случайных чисел, то ГСЧ отлично с этим справятся, но если нужно конкретное значение (скажем 26-е по счёту), то тут вам не повезло. Ну, вы, конечно, можете 26 раз вызвать Next() и использовать последнее число, но это плохая идея.

Зачем мне может понадобиться конкретное число из последовательности?

Если вы генерируете всё и сразу, то такие значения вам, возможно, и не понадобятся, по крайней мере я не смогу придумать для этого причину. Другое дело, если что-то генерируется на лету и по частям.

Скажем, у вас есть три секции игрового мира: A, B, и C. Игрок начинает в секции A, она генерируется с помощью 100 случайных чисел. Затем игрок продвигается в секцию B, которая генерируется 100 других случайных чисел. В это же время секция A уничтожается, освобождая место в памяти. Далее идёт секция C, для создания которой используются другие 100 значений и также удаляется секция B.

Однако, если игрок захочет вернуться в секцию B, её нужно генерировать из тех же значений, что и в первый раз, чтобы она выглядела неизменной.

Могу ли я просто использовать ГСЧ с разными значениями сида?

Нет! Это довольно распространённой заблуждение. Суть в том, что числа одной последовательности случайны по отношению друг к другу, но числа того же порядка из разных последовательностей случайными по отношению к друг другу не будут, даже если так и покажется на первый взгляд.

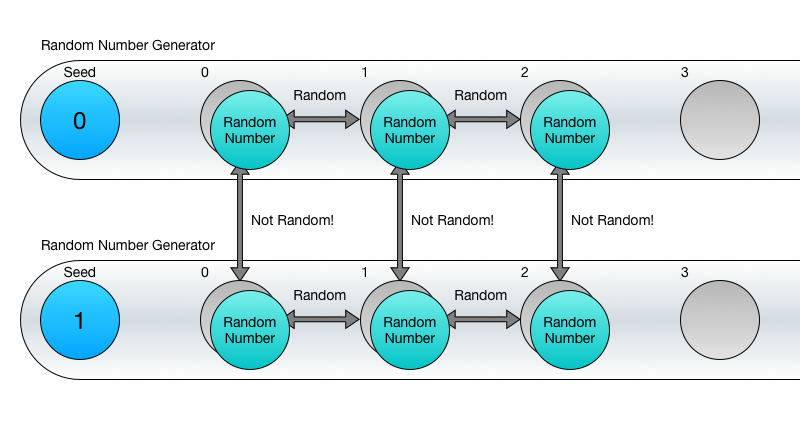
Так что, если взять первые числа из 100 последовательностей, они не будут случайными по отношению к друг другу. Та же картина будет наблюдаться и с 10-ми, 100-ми или 1000-ми порядковыми значениями последовательностей.

К этому моменту многие отнесутся скептически, и это нормально. Можете ознакомиться с этим вопросом на Stack Overflow, если это сильнее вас убедит. Но мы с вами выберем кое-что поинтереснее и поинформативнее и немного поэкспериментируем.

Давайте сравним знакомую нам последовательность с первыми числами из 65536 последовательностей, сгенерированных из сидов от 0 до 65535.

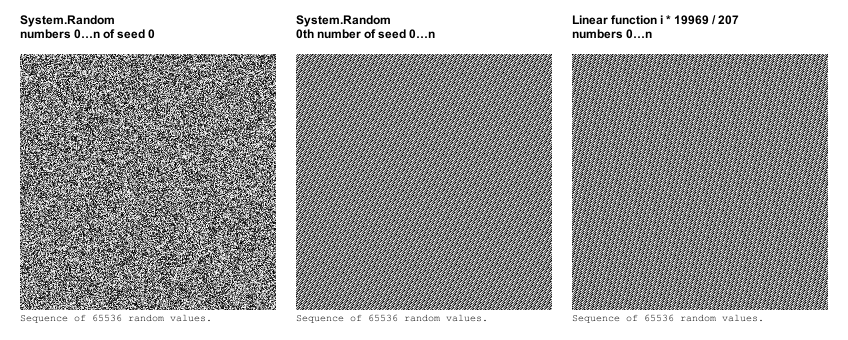
Узор достаточно равномерно распределён, но он не совсем случайный. Для сравнения я разместил рядом результаты из абсолютно линейной функции, и видно, что последовательные сиды выдают числа, по случайности не далеко ушедшие от работы простой линейной функции.

Так ведь они почти случайные? Этого же будет достаточно?

Настало время представить вам способы более точного измерения случайности, потому что не стоит доверять определению на глаз. Но зачем? Разве результат не выглядит достаточно случайным?

В общем-то да, наша конечная цель достаточно достоверно изобразить случайность. Но случайные числа могут совершенно по-разному выглядеть на выходе, в зависимости от области их применения. Ваши алгоритмы генерации могут трансформировать случайные значения любыми способами, выявляя чёткие закономерности, незаметные при простом взгляде на упорядоченную последовательность.

Альтернативным способом проверки случайности результата является создание 2D-координат из спаренных случайных чисел и построение изображения по этим координатам. Чем больше координат попадает на один и тот же пиксель, те ярче он становится.

Давайте взглянем на изображения, полученные таким образом для обычной последовательности и для чисел, взятых из разных последовательностей с разными сидами. Да, и ещё добавим ту линейную функцию.

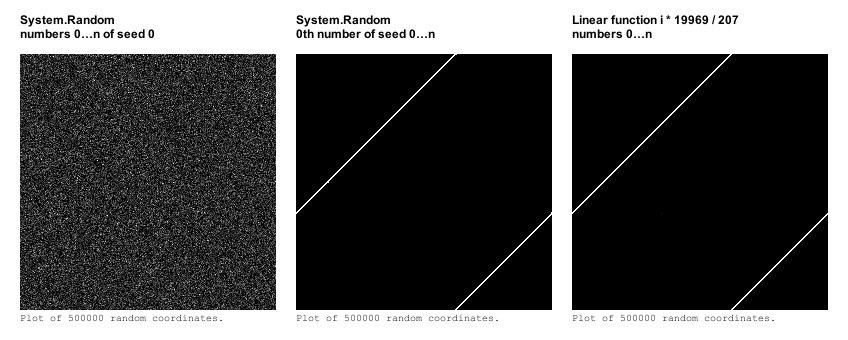
Кого-то, вероятно, удивит, что координаты из последовательностей с разными сидами выстраиваются в тонкие прямые линии, что уже совсем не назвать равномерным распределением. И линейная функция снова выдаёт похожий результат.

Представьте, что вы генерируете координаты для посадки деревьев. Все они будут выстроены в прямые ряды, а остальная местность останется пустой!

Можно заключить, что ГСЧ пригодятся, только если вам не нужен доступ к порядковым значениям последовательностей. В противном случае стоит обратить внимание на случайные хеш-функции.

Случайные хеш-функции

Хеш-функция – это, проще говоря, любая функция для отображения данных произвольного объёма в виде данных фиксированного объёма, где небольшая разница в начальных значениях превратится в большую разницу на выходе.

Основное использование в процедурной генерации – предоставление одного или нескольких целых чисел в качестве входных данных и получение случайного значения в качестве результата. К примеру, в больших мирах, где за один раз генерируется только малая их часть, основная необходимость – получение случайного числа, связанного со входным вектором (таким, как игровая локация), так чтобы это число всегда оставалось неизменным при неизменном входном значении. В отличие от ГСЧ, здесь нет последовательностей – числа можно получать в любом желаемом порядке.

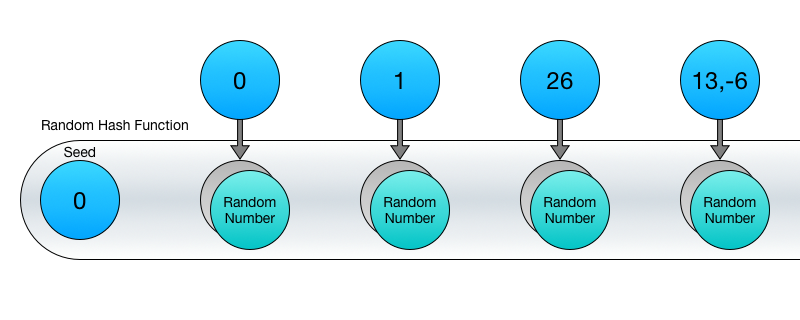
Код на C# будет выглядеть примерно так – обратите внимание, что вы можете произвольно указывать порядок значений:

RandomHash randomHashObject = new RandomHash(12345);
int randomNumber2 = randomHashObject.GetHash(2);
int randomNumber3 = randomHashObject.GetHash(3);
int randomNumber1 = randomHashObject.GetHash(1);

Хеш-функции могут обрабатывать несколько входных значений, то есть, их можно использовать для определённых 2D- или 3D-координат:

RandomHash randomHashObject = new RandomHash(12345);
randomNumberGrid[20, 40] = randomHashObject.GetHash(20, 40);
randomNumberGrid[21, 40] = randomHashObject.GetHash(21, 40);
randomNumberGrid[20, 41] = randomHashObject.GetHash(20, 41);
randomNumberGrid[21, 41] = randomHashObject.GetHash(21, 41);

Процедурная генерация – нетипичное использование хеш-функций, так что не все они будут подходящими, либо выдавая плохое распределение, либо требуя неоправданно много ресурсов.

Одна из традиционных областей применений хеш-функций – реализация структур данных, таких как словари. Зачастую они очень быстрые, но совершенно лишённые элемента случайности, потому что нужны главным образом для более эффективного выполнения алгоритмов.

Другая область их применения – криптография. Такие хеш-функции показывают хорошую случайность, но при этом очень медленные, потому что требования к криптографически стойким функциям гораздо выше, чем к значениям, которые только выглядят случайными.

Нам нужна хеш-функция, которая выглядит случайно, и вместе с тем эффективна, то есть не замедленная ничем лишним. В выбранном вами языке программирования такой может и не найтись, так что придётся подыскивать подходящую для внедрения в проект.

Я протестировал несколько хеш-функций, отобранных на основе рекомендаций со всех уголков Интернета. Для сравнения я выбрал три из них.

• PcgHash: Эту функцию мне порекомендовал Адам Смит (Adam Smith) на форуме Google Groups. Адам предположил, что даже без особых навыков не так уж сложно создать собственную хеш-функцию и предложил свой код PcgHash в качестве примера.
• MD5: Это одна из наиболее известных хеш-функций. Она используется для криптографических нужд и для наших целей слишком затратная. К тому же, нам обычно нужны 32-битные целые значения, тогда как MD5 возвращает гораздо более объёмные числа, большая часть которых будет отбрасываться. Тем не менее, её стоит включить в сравнение.
• xxHash: Это современная высокопроизводительная не-криптографическая функция, проявляющая и хорошие случайные свойства, и отличное быстродействие.

Для тестирования наряду с построением «шумных» изображений и отрисовкой координат я также использовал ENT – Программу Тестирования Псевдослучайных Числовых Последовательностей. Я добавил к изображениям избранные показатели ENT и показатель, который я сам изобрёл и назвал «отклонением диагоналей» – рассматриваются суммы диагональных линий пикселей на отрисовке координат и измеряется стандартное отклонение этих сумм.

Вот результаты по трём указанным функциям:

PcgHash резко выделяется: хоть она и показывает кажущийся случайным результат на шумном изображении, отрисовка координат выявляет чёткий узор, а значит, она плохо справляется с простыми трансформациями. Из этого я могу сделать вывод, что создание собственных хеш-функций – дело нелёгкое, и его, пожалуй, лучше оставить профессионалам.

MD5 и xxHash показывают хорошую случайность, при этом вторая работает в 50 раз быстрее.

Преимущество xxHash ещё и в том, что даже не являясь ГСЧ, она сохраняет концепцию сида, чего не скажешь обо всех хеш-функциях. Возможность указания сида – явное преимущество в области процедурной генерации, потому что с разными сидами вы можете назначать разные случайные свойства объектов, клеток или подобного, а затем просто использовать индекс объекта/координаты клетки в качестве входного значения хеш-функции. Что особенно важно – числа из последовательностей с разными сидами будут случайными по отношению друг к другу (подробности в Приложении 2).

Оптимизация хеш-функций для процедурной генерации

Из проведённых исследований мне стало очевидно, что помимо выбора функции, демонстрирующей высокую производительность в хеш-бенчмарках общего назначения, критически важно оптимизировать её работу под нужды процедурной генерации, не оставляя функцию «как есть».

Вот два основных способа оптимизации:

• Избегайте преобразований между целыми числами и байтами. Большинство хеш-функций общего назначения берут на входе массив байтов и выдают целое либо несколько байтов в качестве результата. Однако, некоторые производительные функции переводят входные байты в целые, потому что оперируют целыми на внутреннем уровне. Для процедурной генерации вполне естественно получать результат хеш-функции на основе целых входящих значений, так что преобразование их в байты бессмысленно. Отказ от использования байтов может утроить производительность, оставляя результат идентичным на 100%.
• Реализация «бесцикличных» методов с одним или несколькими входящими значениями. Большинство хеш-функций общего назначения принимают входные данные переменной длины в форме массива. Это полезно и в процедурной генерации, но нам, как правило, требуется результат на основе 1, 2 или 3 целых чисел. Создание оптимизированных методов, принимающих фиксированное количество значений вместо массива позволяет устранить необходимость в цикле внутри функции, что резко повышает производительность (в 4-5 раз, согласно моим тестам). Я не эксперт в низкоуровневой оптимизации, но подобной разницы можно добиться либо Неявным преобразованием  в цикле for (C# / implicit – for loop имеет в себе условие, как минимум одно, поэтому программа ветвится; нет цикла, нет проблем), либо выделением памяти под массив.

Мои текущие рекомендации сводятся к использованию версии xxHash, оптимизированной для процедурной генерации. Подробнее смотрите в Приложении C.

Мои версии xxHash и других хеш-функций можно найти на BitBucket. Они написаны на C#, но трудностей с портированием на другие языки возникнуть не должно.

Помимо оптимизации, я добавил несколько методов для получения результата в виде целого числа в заданном диапазоне или числа с плавающей запятой в заданном диапазоне, как обычно требуется в процедурной генерации.

Примечание: на момент написания статьи я добавил только оптимизацию единственного целого на входе в xxHash и MurmurHash3. Как будет свободное время, добавлю оптимизацию с двумя и тремя входящими целыми значениями.

Комбинирование хеш-функций и ГСЧ

Генераторы случайных чисел можно комбинировать с хеш-функциями. Разумный подход заключается в использовании ГСЧ с разными сидами, но так, чтобы сиды проходили через случайную хеш-функцию, а не применялись напрямую. Представьте, что ваш мир – это огромный лабиринт, потенциально практически бесконечный. На огромной сетке территории каждая клетка – лабиринт. Пока игрок передвигается по игровому миру, лабиринты генерируются в ближайших клетках.

Если вы хотите, чтобы каждый посещённый лабиринт оставался прежним, вам нужны случайные значения, не основанные на предыдущих из последовательности.

Однако, лабиринты генерируются по одному за раз, так что нет необходимости контролировать порядок случайных чисел в каждом из них.

Идеальным подходом будет использование случайной хеш-функции для генерации сидов лабиринтов на основе их координат и последующее использование сида для генерации последовательности случайных чисел.

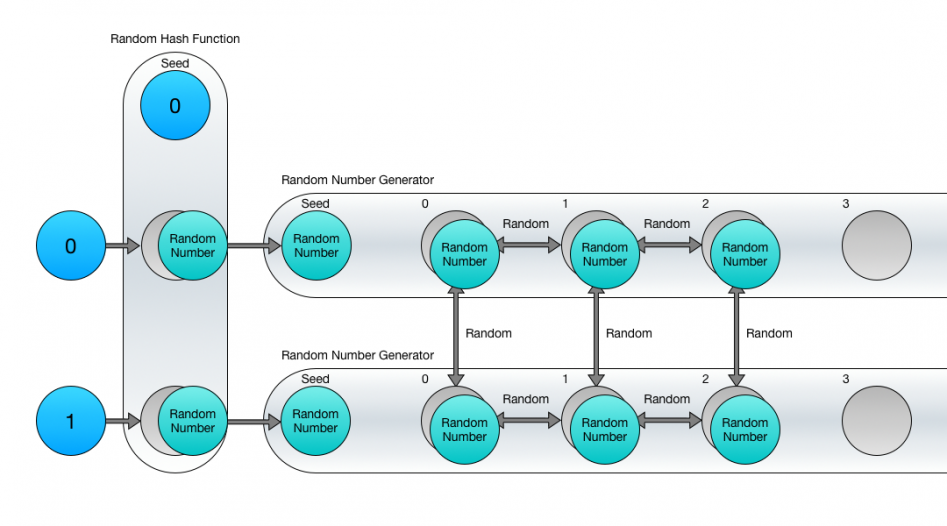
Код на C# будет выглядеть примерно так:

RandomHash randomHashObject = new RandomHash(12345);
int mazeSeed = randomHashObject.GetHash(cellCoord.x, cellCoord.y);

Random randomSequence = new Random(mazeSeed);
int randomNumber1 = randomSequence.Next();
int randomNumber2 = randomSequence.Next();
int randomNumber3 = randomSequence.Next();

Заключение

Если вам нужен контроль над порядком случайных чисел, используйте оптимизированную для процедурной генерации версию подходящей случайной хеш-функции (такую как xxHash).

Если порядок случайных чисел не важен, простейшим способом их получения будет ГСЧ, например класс System.Random в C#. Если все числа должны быть случайными по отношению друг к другу, они должны входить в одну последовательность (инициализированную одним сидом), либо сиды разных последовательностей должны сначала пропускаться через случайную хеш-функцию.

Исходный код вышеупомянутой тестовой среды для случайных чисел, вместе с различными ГСЧ и хеш-функциями, можно найти на BitBucket.

Приложение A: Примечание по продолжительному шуму

В некоторых случаях вам могут потребоваться продолжительные значения шума, то есть близкие по значению входные данные, дающие близкие по значению результаты. Обычно используются для поверхности земли и текстур.

Такое требование кардинально отличается от рассматриваемого в статье. Для продолжительных шумов обращайтесь к функции Perlin Noise или лучше Simplex Noise.

Однако, учтите, что они подходят только для продолжительных шумов. Запрос функций продолжительного шума для получения обычных случайных чисел, не связанных с другими, даст плохие результаты, так как эти алгоритмы оптимизированы для других целей. Например, я заметил, что запрос функции Simplex Noise по позициям целых чисел выдаёт 0 каждый третий раз!

Вдобавок, функции продолжительного шума в своих вычислениях обычно используют числа с плавающей запятой, стабильность и точность которых ухудшаются вместе с отдалением от оригинала.

Приложение B: Результаты дополнительных тестов

На протяжении многих лет я встречаюсь с различными заблуждениями и сейчас попытаюсь разобраться ещё кое с какими из них.

Не лучше ли использовать в качестве сида большие значения?

Нет, я не замечал ничего, что бы на это указывало. Взглянув на результаты тестов в этой статье, вы увидите, что разницы между большими и маленькими значениями нет.

ГСЧ требуется произвести несколько значений, чтобы «разогнаться»?

Нет, как вы видите на тестовых изображениях, последовательности случайных чисел следуют одному узору от начала (верхний левый угол и далее строка за строкой) до конца.

На изображении ниже я сравнил нулевые числа из 65536 последовательностей с сотыми числами из них же. Как видите, заметной разницы между (плохим) качеством случайности нет.

Правда, что некоторые ГСЧ, например в Java, выдают лучшую случайность чисел из последовательностей с разными сидами?

Возможно, чуточку лучше, но она всё равно далека от приемлемой. В отличие от класса Random в C#, класс Random в Java слегка перемешивает биты в сидах перед их сохранением.

Итоговые числа из разных последовательностей выглядят чуть более случайными и мы видим, что показатель серийной корреляции намного лучше. Но на отрисовке координат прекрасно видно, что данные по-прежнему выстраиваются в прямые линии.

На самом деле, я не вижу причин, по которым ГСЧ не используют предварительную обработку сидов высококачественной хеш-функцией. Это выглядит действительно хорошей идеей без каких-либо недостатков. Просто известные мне популярные ГСЧ этого не делают, так что вам придётся воспользоваться описанным мной способом и сделать всё самостоятельно.

Почему для случайных хеш-функций можно использовать разные сиды, а для ГСЧ нельзя?

Нет никакой внутренней причины, но такие хеш-функции, как xxHash и MurmurHash3 рассматривают сид как входное значение, так сказать, применяя к сиду высококачественную случайную хеш-функцию. Благодаря такой реализации всегда можно безопасно использовать n-ное число из последовательности с другим сидом.

Приложение C: Дополнительное сравнение хеш-функций

В оригинальной версии этой статьи я сравнивал PcgHash, MD5, и MurmurHash3 и советовал пользоваться MurmurHash3. MurmurHash3 обладает превосходными свойствами случайности, и приличной скоростью. Её автор также разработал среду тестирования хеш-функций SMHasher, получившую широкое распространение.

Кроме того, я обращался к этому вопросу на Stack Overflow, где сравнивается множество функций и тоже просматривается превосходство MurmurHash.

После публикации Арас Пранкевичус (Aras Pranckevičius) посоветовал мне взглянуть на xxHash, а Нэйтан Рид (Nathan Reed) на Wang Hash, о которой он написал тут.

xxHash смогла победить MurmurHash на её родном поле, показав такие же высокие результаты в SMHasher и при этом демонстрируя гораздо более высокую производительность. Про xxHash можно почитать на её странице на Google Code.

Доработанная мной версия после удаления преобразования байтов оказалась чуть быстрее MurmurHash3, но далеко не настолько, как показано в результатах SMHasher.

Также я поработал с WangHash. Качество случайности оказалось недостаточным, как видно по просматривающимся узорам на отрисовке координат, но зато она в пять раз быстрее xxHash. Затем я испытал WangDoubleHash, скармливающую себе свои результаты, и её качество было отличным и скорость всё ещё втрое быстрее xxHash.

Однако, WangHash (и WangDoubleHash) используют на входе только одно целое число, что побудило меня создать подобные версии xxHash и MurmurHash3. Результат оказался впечатляющим (4-5-кратное увеличение скорости) – настолько, что xxHash сейчас быстрее WangDoubleHash.

Что касается качества, моя тестовая среда показывает заметные недостатки, но она далеко не такая сложная, как SMHasher, а значит, высокие результаты в SMHasher позволяют точнее судить о свойствах случайности, нежели мои собственные тесты. Я бы сказал, что прошедшие мою проверку хеш-функции можно считать эффективными для процедурной генерации, но раз уж xxHash (в своей оптимизированной форме) всё равно быстрейшая из всех функций, прошедших мои тесты, то я могу смело порекомендовать её.

Я бы мог включить в сравнение и другие функции, но сомневаюсь, что результаты xxHash были бы серьёзно превзойдены, поэтому пока что могу спокойно оставить всё так, как есть.

Оригинал находится тут, A Primer on Repeatable Random Numbers.